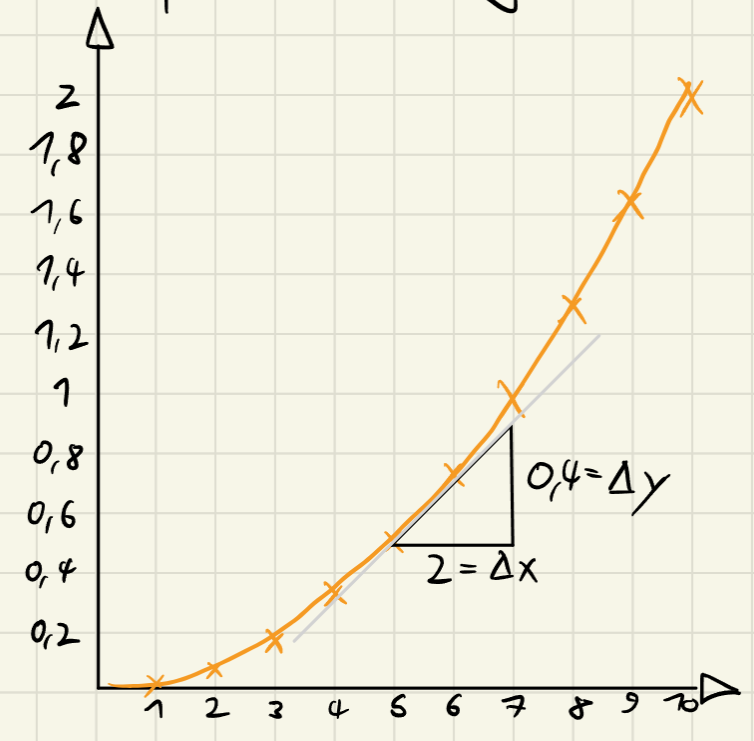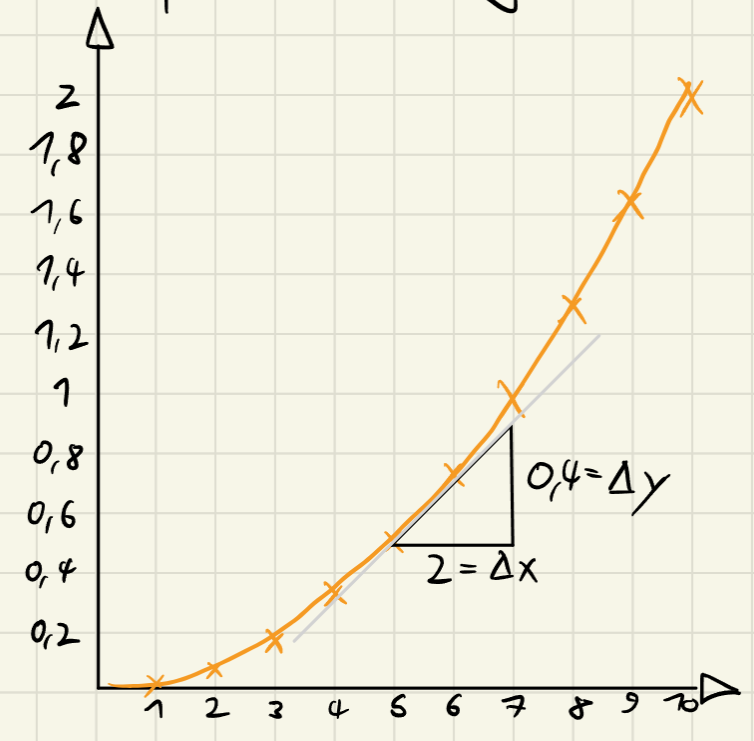Beispiel 1

f(x)=\frac{1}{50} \cdot x^{2} \quad$$Gesucht: Steigung an der Stelle $x_{0}=5$ ## Rechnerische Weg:  1. Ableitung bilden:  $$f^{\prime}(x)=\frac{1}{25} \cdot x

\begin{aligned} x_{0} = 5 in f^{'} (x) einsetzen: f^{'} (5) & = \frac{1}{35} \cdot 5^{1} \\ f^{'} (5) & = 0, 2 \end{aligned}

Graphischer Weg:

\begin{aligned} ⟹ m = \frac{Δ y}{Δ x} m = \frac{0, 4}{2} \\ m = 0, 2 \end{aligned}

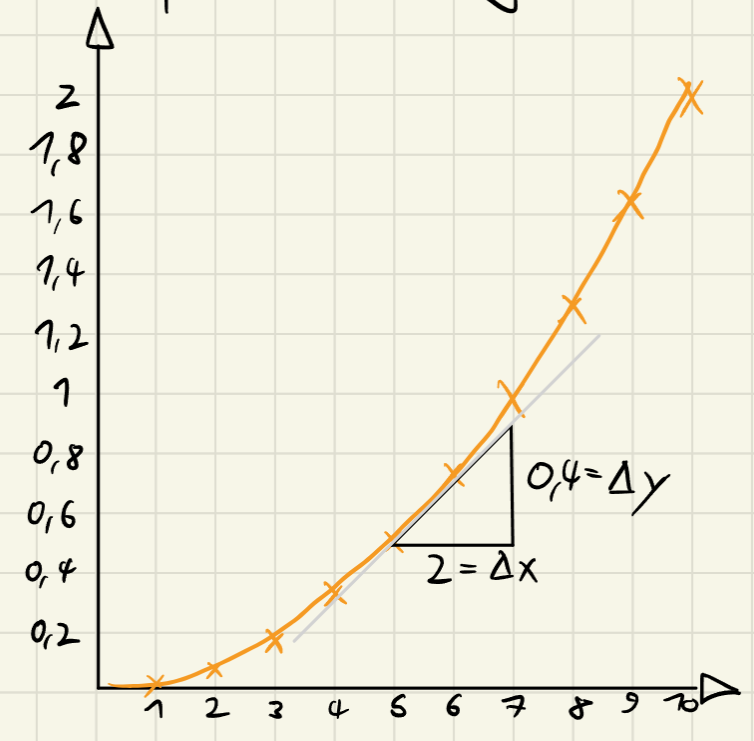
$△$ - Delta = Differenz

Differenzierbarkeit: Steigung ist eindeutig bestimmbar

$⟹ f (x)$ ist stetig und differenzierbar im gesammten Definitionsbereich

f_{a} (x) = {\begin{cases} 2 x^{2} & x < 1 \\ 4 - 2 x & x \geq 1 \end{cases}

$⟹$ stetig, aber für $x = 1$ nicht differenzierbar