7.1 Allgemeines

Natürliche Exponentialfunktion

\begin{array}{ll} g (x) = e^{x} & D_{g} : x \in R \\ W_{g} : g (x) \in R^{+} \end{array}

$⟹$ Umkehrfunktion bilden:

Auflösen/Umformen nach $x$
Umbenennen der Variablen

\begin{aligned} y & = e^{x} ∣ \ln \\ \ln y & = x \\ \ln x & = y \\ f (x) & = \ln x \end{aligned}

Graphen: Eigenschaften von $\ln x$

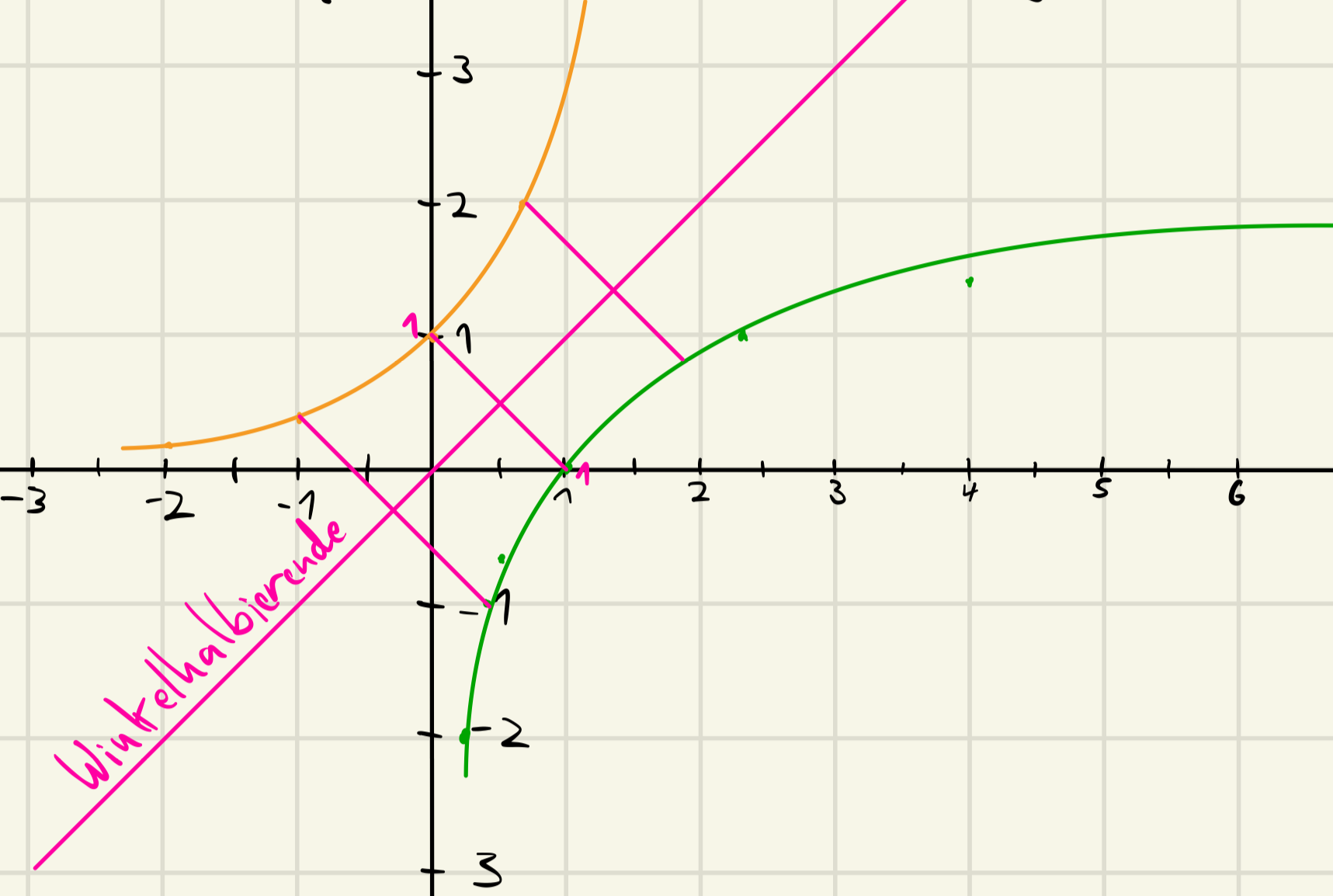
```col-md
![Pasted image 20240426144402.png|300](/img/user/06%20Sources/Anh%C3%A4nge%20Abitur/Anh%C3%A4nge%20Mathematik/Zeichnungen/Pasted%20image%2020240426144402.png)
```
```col-md

$$
\begin{align}
& D_{f}: x \in \mathbb{R}^{+} \\
&\omega_{f}: f(x) \in \mathbb{R} \\ \\
&\ln 1=0 \\
&\ln x<0 \text { für } 0<x<1 \\
&\ln x>0 \text{ für }x>1 \\ \\
& \lim _{x \rightarrow 0}(\ln x)=-\infty \\
& \lim _{x \rightarrow+\infty}(\ln x)=+\infty
\end{align}
$$

```

7.1 Allgemeines

Natürliche Exponentialfunktion

Graphen: Eigenschaften von ln⁡x

Graphen: Eigenschaften von $\ln x$